Chapter 14 of Norman and Streiner has a discussion of the allocation of the sum of squares in multiple regression that does not include specific instructions on how to do that allocation with actual data. The purpose of this web page is to clarify what to do.
Consider $k$ sets of independent variable data points $X_{k,i}$ and dependent variable data points $Y_i$, where $i = 1, ... N$. We are exploring the possibility of a functional relationship between various subsets of the independent variables and the dependent variable, by attempting regressions. To do a regression, we try to find a set of coefficients $b_j$, $j = 0, 1, ... N$ such that ${ \text'χ' }^2 = \text'∑'_i{(Y_i - (b_0 + b_1 X_{1,i} + b_2 X_{2,i} + ... + b_k X_{k,i})^2}$ is minimized, choosing subsets of the independent variables by forcing various $b_j$ to be zero.
The regression is characterized by various sums of squares.
$SS_{reg} = \text'∑'_i{((\text'∑'_j{Y_j})/N - (b_0 + b_1 X_{1,i} + b_2 X_{2,i} + ... + b_k X_{k,i})^2)}$
$SS_{tot} = \text'∑'_i{(Y_i - {(\text'∑'_j{Y_j})/N} )^2}$
$SS_{res} = SS_{tot} - SS_{reg}$
As we change the number of independent variables being fit, $SS_{reg}$ and $SS_{res}$ change, but $SS_{tot}$
remains fixed, so we can explore how much goes to each part for different choices of independent variables.
For a strongly correlated variable or set of variables we expect more of the total to go into $SS_{reg}$
and less into $SS_{res}$. However, when we use more than one variable at a time, we cannot simply add
together the separate values of $SS_{reg}$ to get the value for the two variables used together because
there may be overlap.
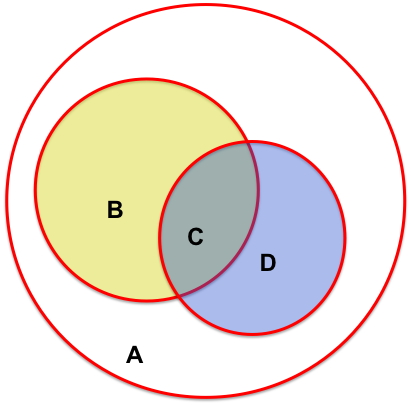
The overlap can be computed by computing $SS_{reg}$ all three ways, once for variable 1, once for variable 2, and once for variables 1 and 2 used togther. Call the three values $SS_{reg,1} = B+C$, $SS_{reg,2} = C+D$, $SS_{reg,1,2} = B+C+D$. $SS_{tot} = A+B+C+D$. The overlap region is $SS_{reg,1} \text'∩' SS_{reg,2} = C$. If we simply add the sizes of $SS_{reg,1}$ and $SS_{reg,2}$ together, we will be counting the size of the overlap region $C$ twice, so
$size (SS_{reg,1} \text'∪' SS_{reg,2}) = size(SS_{reg,1}) + size(SS_{reg,2}) - size(SS_{reg,1,2})$
i.e. $C = (B+C) + (C+D) - (B+C+D)$
We can do similar calculations and diagrams with three variables, but with 4 or more we would need to work algebraically.