5 Brewster Lane, Bellport, New York 11713-2803
Phone: 1-516-286-1339, Fax: 1-516-286-1999
E-mail: yaya@bernstein-plus-sons.com
May 1, 1988
Revised April 26, 1997
The author of this document provides it in the good faith belief that the information
contained therein in correct, but, as with any document, there may be errors and
omissions, and this document may not be applicable in any particular circumstances.
Comments, corrections and suggestions may be directed to yaya@bernstein-plus-sons.com.
Under no circumstances should this document be considered as an alternative to consultation
with appropriately trained professionals.
There are problems with the distributed algorithms. Kleinrock [10] pointed out that "... uncontrolled alternate routing in a congested net can lead to chaos. Indeed, the telephone company tends to limit (and even prohibit completely) alternate routing on unusually busy days (Mother's Day, for example)." As Schwartz notes of a common shortest path algorithm, "Although convergence to the shortest path is guaranteed, routing table entries may change during the convergence period, giving rise to possible loops during that interval," [11, p 277]. Even if one suppresses the creation of loops, there can be serious problems. When the offered load on which routing calculations are being done varies significantly on time-scales commensurate with the convergence period of the routing algorithm, one has created a feedback control system which can oscillate for very long periods. The reader is referred to standard texts on Control Theory, e.g. [1].
In this note, we present a simple example of the type of instability which can result from computing an optimal bifurcated routing for a load which changes on the time-scale of the calculation. While the example was created to clearly demonstrate the sub-optimal results of optimal routing in this case, it is not, in our opinion and observation of the Internet, unrealistic. (The Internet is a loose confederation of networks able to provide a reasonable degree of interoperability for users on connected hosts. See [5].)
As a contrast to optimal routing, we will mention routing found by the Maximum Entropy Method (MEM) [2-4, 8, 9, 12]. MEM, originally due to Jaynes, comes from the interaction of Information Theory with Statistical Mechanics. It works for underdetermined systems, producing the smoothest answer consistent with the data. In the case at hand, it would produce network flows equalized for whatever parameter we wish to smooth: traffic by links, total queue size along paths, etc. Since we need no more than that qualitative approach for our example, we will not present further detail on Maximum Entropy here.
We will form our examples by taking static cascades of independent M/M/1 queues as our model of multi-hop network paths, ignoring blocking, dependence in forwarding, and many other effects. Most importantly, we will ignore the probable failure of stochastic equilibrium by using M/M/1 queuing models even though we vary the customer arrival rate. In a network of large diameter and heavy traffic, it is not unreasonable to assume that the time scales of routing calculations are sufficiently large to consider them as leading to approximate equilibrium queue-by-queue. It would be a good idea to do a more accurate non-equilibrium model, but that would take us beyond our simple pedagogical objective into material better suited to a research paper.
![[image of nodes A,B, C in triangular configuration]](routing1.gif)
We will start with a trivial three-node network. Consider a simple example of a network
consisting of three nodes, A, B, C,
where A has traffic l for B
and may route it either directly or via C.
We assume independent M/M/1 queues at each node, and an equal service
rate 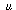 for each queue. We assume that A
supplies a Poisson distributed stream of packets at rate
for each queue. We assume that A
supplies a Poisson distributed stream of packets at rate 
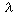 along the direct route and (1 -
along the direct route and (1 -  )
) 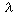 along the indirect route.
Our routing decision is to choose the "best" value of
along the indirect route.
Our routing decision is to choose the "best" value of  .
Assume we seek to control average delay. The average delay is
.
Assume we seek to control average delay. The average delay is
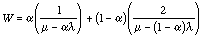
This equation becomes clearer if we define
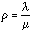
use a dimensionless delay W 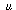 (essentially queue length plus one) and define
(essentially queue length plus one) and define
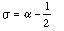
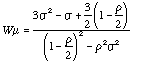
and we seek to minimize W 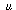 by varying
by varying 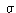 . In this case, it is sufficient to look at the boundary
case
. In this case, it is sufficient to look at the boundary
case  = 1 (
= 1 ( 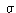 = .5 ) and at the location of zeros of the derivative of W
= .5 ) and at the location of zeros of the derivative of W 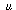 with respect to
with respect to 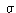 .
.
The zeros of the derivative are given by
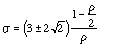
The lower root is the one in the proper range ( -.5 <= 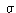 <= .5) as
long as
<= .5) as
long as 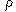 > .293. Below that we use the direct route. Above that value
the routing bifurcates.
> .293. Below that we use the direct route. Above that value
the routing bifurcates.
Consider a situation in which the offered load switches between,
say, 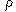 = .3 and
= .3 and 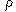 =.9, spending about half its time at each level.
This might be due to the inherent characteristics of the applications,
or, perhaps due to a periodic sensing of overload at the higher load
and a backing off to the light load to relieve congestion. The average load is then
=.9, spending about half its time at each level.
This might be due to the inherent characteristics of the applications,
or, perhaps due to a periodic sensing of overload at the higher load
and a backing off to the light load to relieve congestion. The average load is then
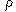 = . 6, and we face the choice of routing for the instantaneous values or for the average.
The "optimum" values of a for these values of
= . 6, and we face the choice of routing for the instantaneous values or for the average.
The "optimum" values of a for these values of 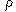 are:
are:
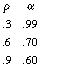
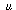 for these values of
for these values of  and for .5 (the Maximum Entropy value, see below).
and for .5 (the Maximum Entropy value, see below).
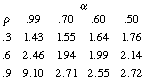
From this table, we observe that the average delay using the optimum a values for the  = .3 and
= .3 and
 =. 9 cases is W
=. 9 cases is W  = 1.99, which is slightly below the average 2.13 of theW
= 1.99, which is slightly below the average 2.13 of theW 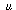 values for alpha .7. We gained about seven percent by using highly dynamic routing. In fact, if we had
used a dynamic shortest path routing, which would have taken
values for alpha .7. We gained about seven percent by using highly dynamic routing. In fact, if we had
used a dynamic shortest path routing, which would have taken  = 1.0
in all these cases, we would have paid a serious delay penalty. Worse yet, suppose
we had a processing time for the dynamic algorithm comparable to the cycle time of
the load and switched to the values of
= 1.0
in all these cases, we would have paid a serious delay penalty. Worse yet, suppose
we had a processing time for the dynamic algorithm comparable to the cycle time of
the load and switched to the values of  for
for 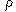 = .3 just
when the load switched to
= .3 just
when the load switched to 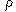 = .9 and vice-versa. Then we would have an average delay for
dynamic routing of W
= .9 and vice-versa. Then we would have an average delay for
dynamic routing of W 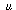 > 5.3.
(For
> 5.3.
(For 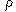 =. 3 we would have used
=. 3 we would have used  = . 6 and gotten a delay ofW
= . 6 and gotten a delay ofW 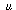 = 1.64,
while for
= 1.64,
while for 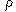 = . 9 we would have used
= . 9 we would have used  = .99 and gotten a delay ofW
= .99 and gotten a delay ofW 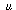 = 9.10). Of further interest is the fact that the Maximum Entropy
value of
= 9.10). Of further interest is the fact that the Maximum Entropy
value of  = . 5 (assuming we balance traffic by links, not paths)
gives a true average delay of W
= . 5 (assuming we balance traffic by links, not paths)
gives a true average delay of W 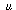 = 2.24 using the correct delay
values of W
= 2.24 using the correct delay
values of W 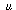 = 1.76 for
= 1.76 for 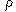 = .3 and W
= .3 and W 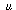 = 2. 72 for
= 2. 72 for 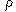 = .9,
a penalty of about fifteen percent for taking too low a value of
= .9,
a penalty of about fifteen percent for taking too low a value of  .
.
If we look at the Maximum Entropy solution for traffic balanced by paths, i.e. making
the average queue on the direct path equal to the average queue on the indirect path,
we obtain bifurcated routing for all values of 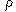 :
:
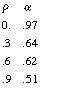
with an average delay for our test case using 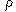 = . 6 for the alternating traffic of 2.10,
a penalty of about five percent. Our conjecture
is that the optimal dynamic routing solutions are, in many cases, similarly unstable
under reasonable dynamic load, and that the Maximum Entropy routings will prove a more robust
starting point for distributed dynamic adjustments.
= . 6 for the alternating traffic of 2.10,
a penalty of about five percent. Our conjecture
is that the optimal dynamic routing solutions are, in many cases, similarly unstable
under reasonable dynamic load, and that the Maximum Entropy routings will prove a more robust
starting point for distributed dynamic adjustments.
![[image of source at rate lambda connected to destination by n paths]](routing10.gif)
 i
i 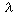 i
goes onto the i th path and sees li hops of servers at rate
i
goes onto the i th path and sees li hops of servers at rate 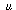 i
i
Thus consider the extension of this analysis to a network with a single client offering
traffic load 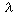 trying to reach a server via n
node-disjoint paths, where each path, i, acts as a cascade of li
independent M/M/1 queues of service rate
trying to reach a server via n
node-disjoint paths, where each path, i, acts as a cascade of li
independent M/M/1 queues of service rate 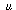 i.
Suppose the client
allocates his traffic to path i
with weight
i.
Suppose the client
allocates his traffic to path i
with weight  i, providing
Poisson distributed traffic at rate
i, providing
Poisson distributed traffic at rate  i
i 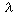 to the path. Then the independent M/M/1 queuing model gives an expected delay of
to the path. Then the independent M/M/1 queuing model gives an expected delay of
![W = sum((alpha[i]l[i])/(mu[i] - alpha[i] lambda)), for 0 <= alpha[i] <= 1, sum(alpha[i]) = 1](routing11.gif)
Define
![d[i] = (alpha[i] l[i])/(mu[i] - alpha[i]l ambda)](routing12.gif)
and compute the partial derivatives which will be needed in finding minima of W .
![partial(d[i])/partial(alpha[i]) = ((mu[i]l[i])/(mu[i] - alpha[i] lambda)^2)](routing13.gif)
for i = 1, ..., n - 1 and
![partial(d[n])/partial(alpha[i]) = ((mu[n]l[n])/(mu[n] - alpha[n] lambda)^2)](routing14.gif)
by taking  n = 1 -
n = 1 -  1 -
1 -  2 - ... -
2 - ... -  n-1,
so that the critical points of W
as a function of
n-1,
so that the critical points of W
as a function of  1, ...
1, ...  n-1, occur when
n-1, occur when
![0 = partial(W)/partial(alpha[i]) = ((mu[i]l[i])/(mu[i] - alpha[i] lambda)^2) - ((mu[n]l[n])/(mu[n] - alpha[n] lambda)^2)](routing15.gif)
i.e. when
![((mu[i]l[i])/(mu[i] - alpha[i] lambda)^2 = tau^2)](routing16.gif)
for some 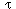 independent of i, i = 1, ..., n.
We will solve these equations for
independent of i, i = 1, ..., n.
We will solve these equations for  i, but first note that
i, but first note that
![mu[i] - alpha[i] lambda = epsilon[i](((mu[i]l[i])^(1/2))/tau)](routing17.gif)
with 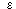 i = +/-1. The negative value of
i = +/-1. The negative value of 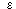 i
is "unphysical", since that would require an overload of the first queue on path i
by the distributed traffic. Thus we accept only the positive roots and obtain
i
is "unphysical", since that would require an overload of the first queue on path i
by the distributed traffic. Thus we accept only the positive roots and obtain
![alpha[i] = (1/lambda)(mu[i] - ((mu[i]l[i])^(1/2))/tau)](routing18.gif)
We can solve for 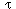 by
by
![1 = sum(alpha[i]) = (1/lambda)sum(mu[i]) - (1/(lambda tau))sum((mu[i]l[i])^(1/2))](routing19.gif)
![tau = sum((mu[i]l[i])^(1/2))/(sum(mu[i]) - lambda)](routing20.gif)
so that
![alpha[i] = (1/lambda)(mu[i]-(sum(mu[j]) - lambda)((mu[i]l[i])^(1/2))/sum((mu[j]l[j])^(1/2))))](routing21.gif)
While all the resulting values of  i are certainly critical
points of W, they may not be valid minima. We can eliminate any
concern about convexity of the problem by noting that
i are certainly critical
points of W, they may not be valid minima. We can eliminate any
concern about convexity of the problem by noting that
![partial(partial(W)/partial(alpha[j]))/partial(alpha[i]) = ((2 mu[i] lambda l[i] delta[i,j])/(mu[i] - alpha[i] lambda)^3) + ((2 mu[n] lambda l[n])/(mu[n] - alpha[n] lambda)^3)](routing22.gif)
which, as the sum of a diagonal matrix with positive terms and a scalar times the
matrix of all ones, is positive definite as long as we have 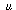 i >
i >  i
i 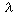 .
(This is only to be expected since this routing problem is one of a much wider class
of convex minimization problems). The real question is whether the minima are within
the region of interest, 0 <=
.
(This is only to be expected since this routing problem is one of a much wider class
of convex minimization problems). The real question is whether the minima are within
the region of interest, 0 <=  i <= 1. We may drive some
i <= 1. We may drive some  i
negative with too small a value of
i
negative with too small a value of 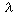 . This corresponds to the
. This corresponds to the 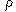 < .293 cases
in our simple example above. In that case, we must reduce the allowed range of i
by dropping appropriate paths.
< .293 cases
in our simple example above. In that case, we must reduce the allowed range of i
by dropping appropriate paths.
To select the paths to be dropped, order the paths so that
![mu[i]/l[i]](routing23.gif)
is monotone non-increasing with i, i.e.
so that the path with the fastest hop-corrected service rate comes first and the slowest
path comes last. Compare 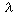 to
to
![sum(mu[i] - (mu[n]/l[n])^(1/2)sum((mu[j] lambda[j])^(1/2))](routing24.gif)
If 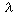 is smaller, drop path n
and recompute on the reduced network, since in that case
is smaller, drop path n
and recompute on the reduced network, since in that case  [n]
will be negative. To see this 0 >
[n]
will be negative. To see this 0 >  [n]
if and only if
[n]
if and only if
![0 > mu[n] - (sum(mu[j] -lambda)(((mu[n] lambda[n])^(1/2))/sum((mu[j] lambda[j])^(1/2)))](routing25.gif)
if and only if
![(mu[n] sum((mu[j] lambda[j])^(1/2)))/(mu[n] lambda[n])^(1/2) < sum(mu[j] - lambda](routing26.gif)
from which the bound on 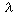 follows.
follows.
We can actually drop more such lines at the same time, since the effect of taking out lines with negative a is to reduce load on other lines, but we cannot assume that the calculation need not be repeated for the reduced set, since we have no assurance that more a will not go negative with this reduced load.
Once we enter a regime in which the critical points are indeed the minima, we can compute the minimal W from
![d[i] = (l[i]/lambda)((mu[i]/l[i])^(1/2)((sum((mu[j]l[j])^(1/2))/(sum(mu[j] - lambda))-1)](routing27.gif)
![W = sum(d[i])](routing28.gif)
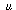 i,j be the service rates of the li
links on path i, reordered so that
i,j be the service rates of the li
links on path i, reordered so that 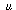 i,1 <=
i,1 <= 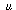 i,j,
j = 2, ..., li.
i,j,
j = 2, ..., li.
![l'[i] = 1 + mu[i,1]sum(1/mu[i,j], j = 2, ... l[i])](routing29.gif)
as the pseudo-hop count to use of links all of rate 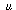 i,1.
The difference between the delay estimated on this path with the pseudo-hop count
and the real delay is
i,1.
The difference between the delay estimated on this path with the pseudo-hop count
and the real delay is
![sum(((1 - (mu[i,1]/mu[i,j]))alpha[i] lambda)/((mu[i,1] - alpha[i] lambda)(mu[i,j] - alpha[i] lambda)), j = 1, ... l[i]) >= 0](routing30.gif)
with equality at  i
i 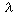 = 0 and for equal service rates.
= 0 and for equal service rates.
2. H. J. Bernstein, Tutorial on Maximum Entropy, Philadelphia, Pennsylvania (6 February 1986). Lecture at the Institute for Cancer Research, Fox Chase Center.
3. H. J. Bernstein, Digital Communications, New Paltz, New York (9 October 1986). Lecture presented in 1986 New Horizons in Physics and Engineering Lecture Series on Telecommu-nications at the College of New Paltz, State University of New York.
4. G. Bricogne, "Maximum Entropy and the Foundations of Direct Methods," Acta Crystallo-graphica, A40 (4), pp. 410-445 (1984).
5. V. Cerf, "The Catenet Model for Internetworking," DARPA/IPTO, IEN-48 (July, 1978).
6. L. Fratta, M. Gerla, and L. Kleinrock, "The Flow Deviation Method: An Approach to Store and Forward Communication Network Design," Networks, 3, pp. 97-133 (1973).
7. M. Gerla, "The Design of Store and Forward Networks for Computer Communications," Ph.D. Thesis, Dept. of Computer Science, UCLA (1973).
8. E. T. Jaynes, "Information Theory and Statistical Mechanics," Physical Review, 106 (4), pp. 620-630 (15 May 1957).
9. E. T. Jaynes, "Information Theory and Statistical Mechanics. II," Physical Review, 108 (2), pp. 171-190 (15 October 1957).
10. L. Kleinrock, "Computer Networks" in Computer Science, ed. A. F. Cardenas, L. Presser & M. A. Marin, pp. 241-284, Wiley-Interscience, New York (1972).
11. M. Schwartz, Telecommunications Networks, Addison-Wesley Publishing Company, Read-ing, Massachusetts (1987).
12. C. E. Shannon, "A Mathematical Theory of Communication," The Bell System Technical Journal, XXVII (3), pp. 379-423, 623-656 (July 1948).